'Carrollian' bir kara tahta

Geçtiğimiz haftaki 6 tam temaslı sigara, şekilde gösterilen düzenlemeyle geliştirilebilir; burada yedinci sigara, diğerlerinin oluşturduğu merkezi boşluğa yerleştirilir.

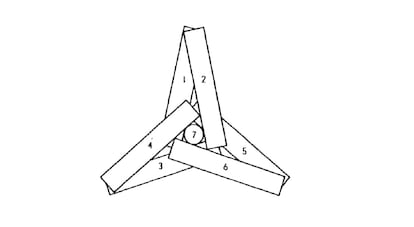
(Bildiğim kadarıyla) henüz kanıtlanmamış olan şey, 7'nin mümkün olan en yüksek değer olduğudur (her ne kadar şeklin çözümünün tek olmadığı gösterilmiş olsa da, bunu daha sonra göreceğiz).

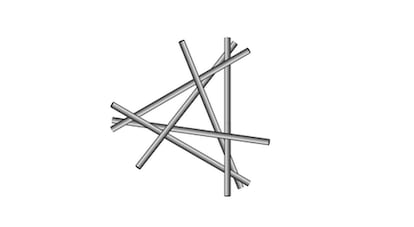
Sonsuz uzunluktaki sigaralara -ya da silindirlere- gelince (bu türev, İngiliz matematikçi John Littlewood tarafından önerilmiştir), bunlar herhangi bir çözüm sunmadığından, dikkatli okuyucularımın dikkatini çekmemiştir. Dikkat meselesi olmasa da zorluk meselesi olabilir, çünkü bunun hiç de kolay olmadığını kabul etmek gerekir: Şekilde, yakın zamana kadar aşılmaz sanılan 6 silindirli bir çözüm görülüyor, 7 silindirli iki farklı çözüm bulundu (ki bu, elbette sonlu sigaralar için de geçerlidir). Şekle dikkatlice bakıp, buradan yola çıkarak siz de bu çözümlerden birini bulabilirsiniz; Ama sabırlı olun, çünkü varlığını bilmek her şeyi kolaylaştırsa da, yine de çok zordur.

Ve sert silindirlerden esnek silindirlere doğru ilerlerken, öncekilerin zorluğunu telafi etmek için basit bir problem:

2 mm çapında dairesel kesite sahip 1 metre uzunluğunda bir lastiğimiz var. Kesit çapı 1 mm olana kadar gerersek ve deformasyonun kauçuğun tüm uzunluğu boyunca aynı olduğunu varsayarsak, şimdi uzunluğu ne kadar olur ? Ve çözümü bulduktan sonra onu "pişirmeyi" deneyin.

Gerilme ile büzülme arasındaki ilişkiye Poisson oranı denir ve çoğu malzemede pozitiftir (gerilme ne kadar fazlaysa büzülme de o kadar fazla olur); Ancak auxetic adı verilen bazı malzemeler negatif Poisson oranına sahiptir, yani gerildiklerinde genişlerler.

Genişletilmiş politetrafloroetilen (diğer markaların yanı sıra Gore-Tex olarak pazarlanmaktadır) gibi sentetik oksetik malzemelerin birçok uygulaması vardır ve tesadüfen (matematikte ve makroskobik fizikte hiçbir şey tesadüf değildir) karşılıklı temas halindeki maksimum sayıda iplik (pratik amaçlar için sonsuz silindirler) oksetik ağların üretiminin temelini oluşturur ve bu da araştırmacıları mümkün olan maksimum değeri aramaya yöneltmiştir. Matematikçilerden önce keşfettikleri sayının 7 olduğu ortaya çıktı.

Öklid dışı bir kara tahta mı?

Geçtiğimiz haftaki ana çizimde yer alan iki kızın, tahtaya yazdıklarına bakılırsa, matematikte pek iyi olmadıkları anlaşılıyor. Ama onları yargılamakta fazla aceleci olmayalım: Belki alışılmadık terimlerle ifade edilmişlerdir ama bu onların yanlış olduğu anlamına gelmez. Ya da belki de Lewis Carroll'ın, genç kızları saçmalıklarıyla şaşırtmayı çok seven, kendi uydurduğu matematiksel bir şakanın konusu olmuşlardır. 180 = 90 + 30 eşitliğinin anlamlı olma ihtimali var mıdır?

Öte yandan, Öklid düzleminde bir üçgenin açılarının toplamı en fazla 180º'dir; başka bir yüzeyde toplamları ikiden fazla veya az dik açıya eşit olabilir (açıları toplamı 270º olan bir üçgen çizebilir veya tarif edebilir misiniz?).

Tahtadaki üçgene gelince, gizli açının her zamanki işaretini gördüğümüzden dik açılı olduğunu biliyoruz, ancak değerini göremiyoruz (sadece son 0 görünüyor); ama tizlerin değerini görüyoruz: sırasıyla 40º ve 30º. Gizli dik açıya, şekli anlamlı kılacak bir değer vermek mümkün müdür?

Ve geçen haftaki çizimden yola çıkarak metne geçip küçük bir meta-problem sorabiliriz: Otomatik yazım denetleyicisinin ünlü Fransız matematikçi ve fizikçi Poisson'un adını italik yapmasının mantıksal nedeni ne olabilir?