Leonardos Weltkarte

Die Fläche des Reuleaux-Dreiecks (R) aus der letzten Woche ist gleich der Fläche des gleichseitigen Dreiecks mit der Seite 1 (T) plus dem Dreifachen der Fläche des Kreissegments (S) auf jeder Seite:

R = T + 3S, wobei S der Kreissektor abzüglich des Dreiecks ist:

S = π/6 – T, dann

R = T + 3(π/6 – T) = π/2 – 2T

T = √3/4

R = (π - √3)/2

Einige Leser haben darauf hingewiesen, dass es auch Münzen in Form von Reuleaux-Polygonen gibt. Die bekannteste ist zweifellos die britische 50-Pence-Münze, die ein Reuleaux-Heptagon darstellt.

Die letzte Woche gestellte Frage, ob es Reuleaux-Polygone (d. h. Polygone konstanter Breite) gibt , die aus unregelmäßigen Polygonen oder Polygonen mit einer geraden Anzahl von Seiten konstruiert werden können, lautet ja; allerdings sind in diesem Fall die Bögen des resultierenden Polygons nicht alle gleich oder haben nicht die gleiche Krümmung.

Einer der weniger bekannten, aber nicht minder wichtigen Aspekte von Leonardo da Vincis Werk ist sein Beitrag zur Kartografie. In seinem Sammelband, dem Codex Atlanticus , der in der Biblioteca Ambrosia in Mailand aufbewahrt wird, findet sich ein Manuskript aus dem Jahr 1508, in dem Leonardo die verschiedenen damals bekannten Kartenprojektionen analysiert, darunter die planare Kegelprojektion des Ptolemäus und die Planisphäre von Contarini-Rosselli, und eine neue einführt. Diese neue Projektion besteht darin, die Erdkugel in acht Oktanten zu unterteilen und diese anschließend zu Reuleaux-Dreiecken abzuflachen. War dies eine willkürliche oder rein ästhetische Entscheidung, oder ergibt das Abflachen eines Oktanten einer Kugel zwangsläufig ein Reuleaux-Dreieck?

Leonardo gruppierte die vier Oktanten jeder Hemisphäre zu einer Art vierblättrigem Kleeblatt, wobei sich die Pole in den jeweiligen Zentren der Kleeblätter befanden. So entstand die sogenannte „Leonardo-Weltkarte“, deren Urheberschaft jedoch nicht sicher ist (einige vermuten, dass sie später von einem seiner Assistenten gezeichnet wurde). Sicher ist jedoch, dass das Renaissance-Genie als Erster die Projektion in Oktanten und deren Gruppierung in zwei vierblättrige Kleeblätter vorschlug, wie unter anderem eine Skizze des bereits erwähnten Manuskripts von 1508 im Codex Atlanticus belegt.

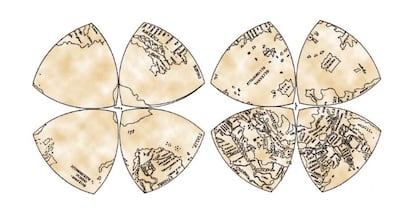
Es ist wichtig zu beachten, dass die Oktantenprojektion weder winkeltreu noch flächentreu ist. In der Kartografie erhält eine winkeltreue Projektion Winkel (oder zumindest die meisten davon), wie beispielsweise die Mercator- oder die stereografische Projektion. Eine flächentreue Projektion hingegen bewahrt die Flächenverhältnisse verschiedener Länder oder anderer dargestellter geografischer Regionen. Je nach Art der zu erstellenden Karte können weitere Merkmale wie die Form verschiedener geografischer Gebiete, Entfernungen, Richtungen usw. erhalten bleiben. Manchmal bedeutet die Erhaltung einer dieser Variablen die Verzerrung anderer. Kann eine Kartenprojektion sowohl winkeltreu als auch flächentreu sein? Wie?

Und zum Schluss stelle ich meinen aufmerksamen Lesern eine Frage, die zwar botanisch anmuten mag, aber rein logisch ist: Gibt es vierblättrige Kleeblätter?