Die drei Figuren

Zu Punktrastern, einem wiederkehrenden Thema, das letzte Woche erneut aufkam, sagt Salva Fuster: „Ich würde sagen, dass wir bei einem nxn-Raster alle Punkte verbinden können, ohne den Stift vom Papier abzusetzen oder zweimal über dieselbe Linie zu fahren, und zwar mit 2(n-1) geraden Linien. Eine Ausnahme bildet das 2x2-Raster, für das drei Linien erforderlich wären. Allerdings müsste nachgewiesen werden, dass dies mit weniger Linien nicht möglich ist.“

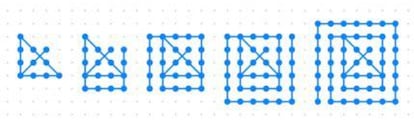
Übrigens gibt es für das 4x4-Gitter eine andere Lösung als die in der Abbildung gezeigte, bei der mehrere Eckpunkte der gestrichelten Linie außerhalb des Gitters liegen. Können Sie sie finden? (Tipp: Es ist eine elegante symmetrische Lösung.)

Und in Bezug auf das Rechteck und die beweglichen Teile sagt Rafael Granero: „C bewegt sich zur Mitte seiner langen Seite (parallel zu AB).

B bewegt sich parallel zur neuen Linie AC, bis es auf gleicher Höhe mit der Seite ist, auf der C liegt, und richtet sich somit mit C aus. A bewegt sich parallel zur Linie BC, bis es auf halber Strecke ihrer langen Seite ist. Und jetzt haben wir die Punkte A und C auf halber Strecke der langen Seiten und B entlang der Hügel von Úbeda.“

Und B bleibt dort, egal was wir tun, da es unmöglich ist, die drei Teile an den Mittelpunkten von drei Seiten des Rechtecks ​​zu platzieren. Wenn sich einer der Scheitelpunkte parallel zu der von den beiden anderen festgelegten Linie bewegt, bleibt die Fläche des Dreiecks ABC konstant, da weder die Basis noch die Länge der Höhe variieren und ihr Wert 1/2 der Fläche des Rechtecks ​​beträgt, während die Fläche eines Dreiecks, dessen Scheitelpunkte an den Mittelpunkten von drei Seiten liegen, 1/4 der Fläche des Rechtecks ​​betragen würde.

Bezüglich der Radien einbeschriebener Kreise schlägt Luis Ortiz einen genialen Ansatz vor: „Die Radien der einbeschriebenen Kreise eines Dreiecks mit den Seiten 3, 4 und 5 haben die Längen 2, 3 und 6, ein Problem, das im Folgenden mithilfe von Gleichungen gelöst wird. Die Seiten des Dreiecks erfüllen den Satz des Pythagoras, es handelt sich also um ein rechtwinkliges Dreieck. Die Katheten werden so ausgelegt, dass sie mit den x- und y-Achsen eines kartesischen Systems zusammenfallen, sodass die Eckpunkte des Dreiecks die folgenden Koordinaten haben: A(0,0), B(4,0) und C(0,3)“. Von hier an ist der Beweis einfach (ich führe ihn aus Platzgründen nicht vollständig an).

Überall Kreise, Dreiecke und Rechtecke

In den letzten Wochen haben wir über Kreise, Dreiecke und Rechtecke gesprochen, die zufällig (oder vielleicht auch nicht) die drei geometrischen Figuren sind, die wir überall sehen.

Die Allgegenwärtigkeit von Rädern auf allen Fahrzeugtypen in unserer motorisierten Gesellschaft würde ausreichen, um die Vorherrschaft der Kreise zu erklären; wir finden sie jedoch auch auf vielen anderen Objekten, wie etwa auf Glas- und Kanaldeckeln oder Säbelklingen.

Es ist offensichtlich, dass Fahrzeugräder und die Deckel vieler Gläser rund sein müssen, da sie sich selbst ausrichten müssen; Kanaldeckel könnten jedoch quadratisch, rechteckig oder elliptisch sein. Es gibt jedoch mindestens drei zwingende Gründe (Wortspiel beabsichtigt) dafür, dass sie rund sind. Welche drei Gründe sind das? Oder gibt es mehr als drei?

Und ohne ein Experte für Klingenwaffen sein zu müssen, können wir mit Sicherheit sagen, dass die Krümmung einer Säbel- oder Katanaklinge einem Kreisbogen entspricht. Warum?

Was Dreiecke betrifft, gibt es einen zwingenden Grund (Wortspiel beabsichtigt), warum wir sie ständig in allen möglichen Strukturen sehen, von Strommasten bis hin zu geodätischen Kuppeln, einschließlich des Eiffelturms selbst. Was ist dieser zwingende Grund?

Und es ist kein Zufall, dass Kisten, Ziegel, Wände, Blätter Papier und so viele andere Dinge rechteckig (oder orthoedrisch, was in 3D dasselbe ist) sind. Le Corbusier sagte sogar, der rechte Winkel sei unser Solidaritätspakt mit der Natur. Was meinte er damit?